LaTeX—pgfplots宏包入门使用教程
- 科普文章
- 2022-10-02 13:39
- 4665
- 0赞
pgfplots 宏包简介以及示例
Pgfplots是一种可视化工具,可简化在文档中包含绘图的过程。基本思想是,用户提供输入数据/公式,然后pgfplots 宏包会帮助用户绘制响应的图像。
我一般使用pgfplots 宏包绘制函数图像。
像使用其他宏包一样,首先我们也需要在导言区调用pgfplots 宏包:
\documentclass{article}...\usepackage{pgfplots}...\begin{document}...\end{document}
pgfplots 宏包可以帮助用户绘制2D 和3D 的函数图像,比如我想要绘制一个2D 的函数图像 ,那我们可以这样操作:
%Ex1:f(x)=exp(x)\begin{tikzpicture}\begin{axis}\addplot[color=red]{exp(x)};\end{axis}\end{tikzpicture}
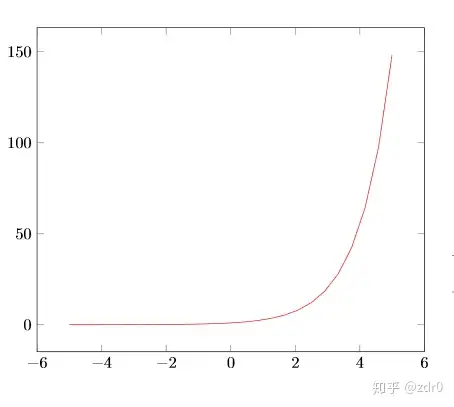 图片1:Ex1:f(x)=exp(x)。
图片1:Ex1:f(x)=exp(x)。
由于pgfplots基于tikz,因此该图必须置于tikzpicture 环境中。然后环境声明\begin {axis}...\end {axis}将为绘图设置正确的缩放比例。该环境相当于创建了坐标系。
要绘制图像,我们需要使用命令:
\addplot[option] {expression of 2D function};
在方括号内可以传递一些选项,比如我们可以像Ex1一样,将函数图像的颜色设置为红色。我方括号是必需的,如果没有传递任何选项,则方括号之间留有空白即可。在花括号内,我们要填写的2D 函数的表达式,比如在Ex1中,我们所写的表达式是 。最后最重要的是该命令必须以分号 ; 结尾。
如果想要要在第一个图旁边放置第二个图,那么声明一个新的tikzpicture 环境即可。不要插入新行,而是插入一个小的空格,比如 \hskip 10pt 将插入一个10pt 宽的空格。
举了一个2D 图像的例子,那我们呢在举一个3D 图像的例子好了,我们就按上述方法将这两个图像放在一起:
%Ex2: put the 2D plot and the 3D plot together\begin{tikzpicture}\begin{axis}\addplot[color=red]{exp(x)};\end{axis}\end{tikzpicture}%Here ends the furst 2D plot\hskip 10pt%Here begins the 3d plot\begin{tikzpicture}\begin{axis}\addplot3[
surf,
]{exp(-x^2-y^2)*x};\end{axis}\end{tikzpicture}
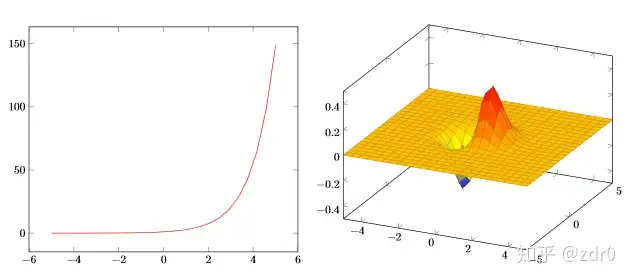 图片2:Ex2:put the 2D plot and the 3D plot together。
图片2:Ex2:put the 2D plot and the 3D plot together。
在Ex2 绘制3D 图像 时,除了:
\addplot3[
surf,
]{exp(-x^2-y^2)*x};
其余部分均与绘制2D 图像时的语法是一致的。这里命令\addplot3 命令是绘制3D 图像的命令。方括号内的选项surf 声明这是一个曲面图。要绘制的函数表达式必须放在大括号内。同样,不要忘了在命令的末尾加上分号 ; 表示该命令结束。
我们在导言区调用了pgfplots 宏包之后还可以进一步进行一些调整。要更改每个绘图的大小并确保向后兼容(推荐),我们可以这样做:
\pgfplotsset{width=10cm,compat=1.9}
做这会将每个pgfplot图形的大小更改为10cm,10cm在这里是一个很大的长度;用户也可以使用不同的单位比如磅,毫米,英寸等等。
由于 诞生初期并未考虑使其具备绘图功能,因此当文档中有多个pgfplot图形或它们非常复杂时,渲染它们将花费大量时间。为了缩短编译时间,用户可以配置软件包以将图形导出为单独的PDF文件,然后将其导入文档中,即我们呢可以将以下代码添加到导言区中:
\usepgfplotslibrary{external}\tikzexternalize
2D 图像绘制
2D 函数图像
Pgfplots 2D绘图功能十分强大和丰富,用户可以个性化绘图以准确显示所需的内容。而且,默认选项通常也会产生很好的结果,因此大多数情况下用户要做的就是输入数据,剩下的工作全都丢给 就好了。
在第一小节中我们已经举过一个例子了,这里我们在举几个更具体的绘制2D 函数图像的额例子,这里例子中的内容会更加丰富。
%Ex3\begin{tikzpicture}\begin{axis}[
xlabel=$x$,
ylabel={$f(x) = x^2 - x +4$}]\addplot {x^2 - x +4};\end{axis}\end{tikzpicture}
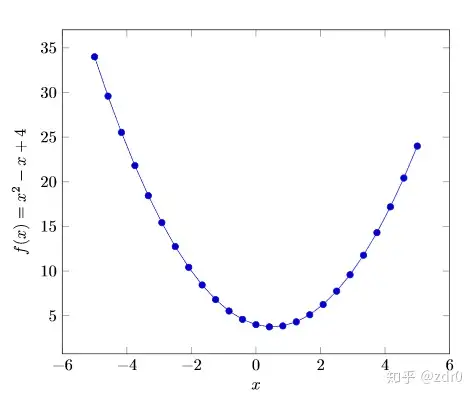 图片3:Ex3.
图片3:Ex3.
在Ex3 中,我们绘制了函数 我们为坐标轴添加了一些信息:
:为 轴添加文本;
:为 轴添加文本。
我们将文本内容放在大括号中即可。
%Ex4\begin{tikzpicture}\begin{axis}[
axis lines = left,
xlabel = $x$,
ylabel = {$f(x)$},
]%Below the red parabola is defined\addplot [
domain=-10:10,
samples=100,
color=red,
]{x^2 - 2*x - 1};\addlegendentry{$x^2 - 2x - 1$}%Here the blue parabloa is defined\addplot [
domain=-10:10,
samples=100,
color=blue,
] {x^2 + 2*x + 1};\addlegendentry{$x^2 + 2x + 1$}\end{axis}\end{tikzpicture}
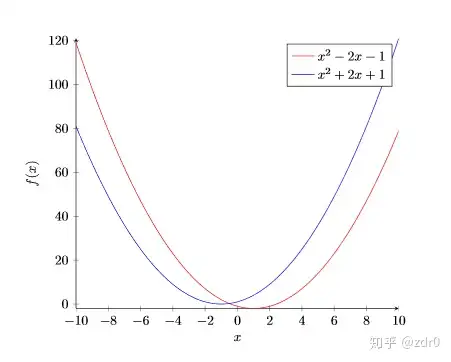 图片4:Ex4.
图片4:Ex4.
:这个命令会仅在图的左侧和底部设置轴,即我们的平面直角坐标系,而不是像我们在图片3中看到的那种默认框;
:设置 的范围为 。即只绘制函数在 之间的图像;
:类似于采样。确定域定义的间隔中的点数。样本值越大,用户获得的图形越锐利,但是渲染所需的时间更长;
:该命令可以为我们所绘制的函数图像添加相应的标签。
标签的位置是可以调整的,下例告诉了我们如何调整标签:
%Ex5\begin{tikzpicture}\begin{axis}[legend pos=outer north east,
xlabel=$x$,
ylabel=$f(x)$]\addplot [red] {sin(deg(x))};\addplot [blue,samples=201] {cos(deg(x))};\legend{$\sin(x)$,$\cos(x)$}\end{axis}\end{tikzpicture}
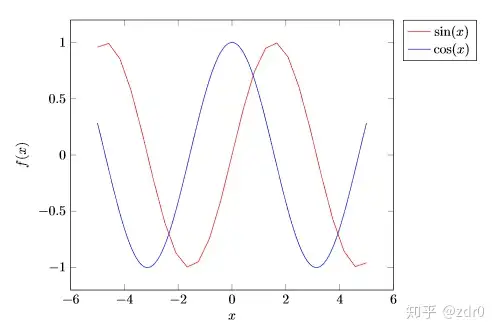 图片5:Ex5.
图片5:Ex5.
在Ex5 中,我们可以在axis 的头部设置标签的位置(legend position)。即:
:outer 表示将标签放在坐标系的外面,north east 是将标签放在图像的东北方向上,即右上角;
:同时为函数1和函数2添加标签。
而且我们在图片5中我们发现 经过采样之后变得更光滑了。且 是将 转化为弧度制。
最后我们来画几个正态分布的图像作为练习吧!
要求:绘制图像 ,请使用普通的平面直角坐标系,并使用不同颜色对不同的曲线进行区分,并将标签置于坐标轴外侧东北方向上,并对横轴和纵轴分别添加文本 ,采样值均设置为 。
答:
\begin{tikzpicture}\begin{axis}[
legend pos=outer north east,
axis lines = left,
xlabel=$x$,
ylabel=$f(x)$]\addplot [
domain=-3:3,
samples=100,
color=red,
]{exp(-x^2)};\addplot [
domain=-3:3,
samples=100,
color=blue,
]{exp(-x^2/2)};\addplot [
domain=-3:3,
samples=100,
color=green,
]{exp(-x^2/3)};\addplot [
domain=-3:3,
samples=100,
color=orange,
]{exp(-x^2/4)};\legend{$\exp(-x^2)$, $\exp(-x^2/2)$, $\exp(-x^2/3)$, $\exp(-x^2/4)$}\end{axis}\end{tikzpicture}
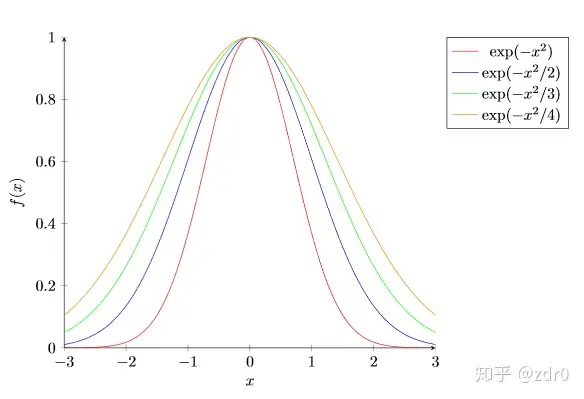 图片6:练习题绘制结果。
图片6:练习题绘制结果。
数据图
科学研究通常会产生必须分析的数据。下一个示例向我们展示的是如何使用pgfplots 绘制数据图。
%Ex6:plot from data\begin{tikzpicture}\begin{axis}[
title={Temperature dependence of CuSO$_4\cdot$5H$_2$O solubility},
xlabel={Temperature [\textcelsius]},
ylabel={Solubility [g per 100 g water]},
xmin=0, xmax=100,
ymin=0, ymax=120,
xtick={0,20,40,60,80,100},
ytick={0,20,40,60,80,100,120},
legend pos=north west,
ymajorgrids=true,
grid style=dashed,
]\addplot[
color=blue,
mark=square,
]
coordinates {
(0,23.1)
(10,27.5)
(20,32)
(30,37.8)
(40,44.6)
(60,61.8)
(80,83.8)
(100,114) }; \legend{CuSO$_4\cdot$5H$_2$O}
\end{axis}\end{tikzpicture}
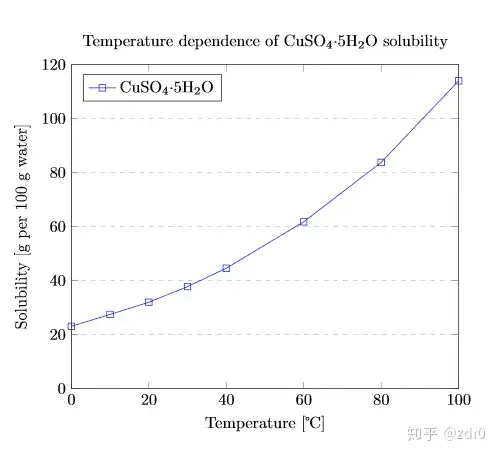 图片7:Ex6:plot from data。
图片7:Ex6:plot from data。
:由于我们的tikzpicture 环境不属于浮动环境所以如果我们想要对我们所绘制的图像添加标签的话那我们就需要使用 ,其后面的 中填写文本,即我们想要给这幅图取的名字;
:设置 的最小值为 ,最大值为 ;设置 的最小值为 ,最大值为 ;
:标记放置的点。如果为空,则自动设置刻度线。即分割坐标轴;
:启用/禁用 轴上刻度线位置上的网格线;
:将网格线的类型设置为普通线性虚线;
:将所要被标记的点绘制成为一个正方形标记。每个标记的点将通过